Cladded Rod

We receive from Tim Beeman of Fiberoptics Technology Inc. a sample of 1.2-mm diameter clad rod. The core of the rod is made of Schott glass type F2, with refractive index 1.63 for blue light and 1.61 for red. The cladding is Schott 8250 glass with index 1.49. We expect the numerical aperture of the rod to be 0.66 for blue light and 0.61 for red.

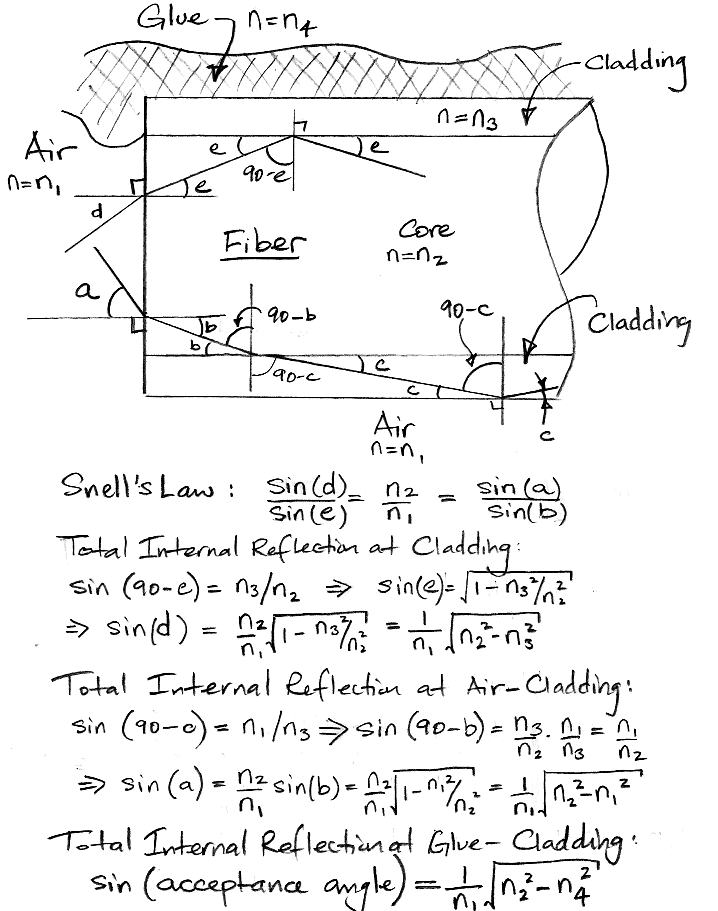
We cut a 200-mm length and cover it with black epoxy of refractive index 1.5 for half of its length. We polish both ends with diamond grit paper to give an optical finish. The epoxy makes sure no light gets into the rod through its curved surfaces. It mimics the epoxy we have been using to bind our fiber to our LED, and makes sure that the cladding of the rod is what causes total internal reflection in the core, rather than the cladding-air interface. We set up the cladded rod as shown below, with a 650-nm red laser beam shining into one end, and a screen to observe the pattern of light emitted by the far end. We place a black foam baffle around the near end of the rod.



The light entering the rod emerges in a cone, making a ring on our screen. When a light ray enters a cylindrical rod at an angle θ to the axis, reflections off the rod surface re-direct the ray, but do not change the angle it makes with the axis. When the ray emerges from the rod, after many reflections of a perfectly-cylindrical rod, it emerges at an angle θ to the axis. We see two cones for small angles of incidence, but in the photograph we are at 40° and the ring is clear and sharp. With a photodiode and our graduated screen, we measure the power emerging from the end of the rod and the angle of the cone it emits. We obtain the following graphs.



Our measurement of transmission becomes unreliable for angles bigger than 60° because the rod end presents such a small area to the laser beam. Nevertheless, we see that the rod captures and transports more than 50% of the light incident upon one end for angles 60° and lower. With numerical aperture 0.61, we expect to get total internal reflection within the rod for angles less than 38°. We see 80% transmission at 40° and 25% at 60°. We believe these results are consistent with numerical aperture 0.61.

If we could obtain such a rod with diameter 400 μm, its numerical aperture for blue light would be 0.66. With such a fiber we could capture 43% of light emitted by our LED and transport it to the fiber tip. If we coat this rod with a layer of adhesive with index 1.32, the coated rod will have numerical aperture 0.96. It will capture and transport almost all the light that enters its base from our LED.

UPDATE: [27-MAR-13] Fiberoptics Technology tells us they can make 400-μm clad rod of the same type studied here. We have ordered a batch to arrive in a few weeks. The company tells us that they believe they can make the same diameter clad rod out of glass with index 1.75. When combined with their cladding, a core of index 1.75 provides numerical aperture 0.92, with no need to use low refractive index adhesives.

UPDATE: [15-APR-13] We try out a Luxeon Z LED, the blue LXZ1-PB01 version. The LED emits roughly 29 mW for 30 mA forward current. The emitting surface of the LED is 1.2 mm square. We place our 1.2-mm diameter, 200-mm long clad rod over it and observe roughly 40% of the power emerging from the other end. The rod covers 80% of the emitting surface of the LED, so it appears that the rod is transporting 50% of the light that enters its base.

UPDATE: [16-APR-13] We receive several hundred meters of clad rod from Fiberoptics Technology. Its diameter is 390 μm. We can bend it with into a radius of 10 cm. We take a 20-cm length, polish both ends, and glue one end to our LXZ1-PB01 blue LED. We use UV-curing adhesive of refractive index 1.54. We coat most of the length of the rod in the same adhesive. We run 30 mA through the LED, so that it emits 29 mW. The rod covers 8.3% of the emitting area of the LED, so we expect 2.4 mW to enter the base of the rod. If the numerical aperture of the clad rod is 0.66, we expect 44% of the light to reach the other end, or 1.0 mW. We measure 1.4 mW at the other end. We press the rod tip against a piece of white paper so we can see the cone of light it emits. The angle at the base of the cone is roughly 74°, which suggests a numerical aperture of 0.60.

Fiber-Cladding Adhesive

When we make a Head Fixtures (A3024HF), there is a stage at which we have the 7-mm long, tapered fiber positioned above the bare LED, ready to be glued in place with clear epoxy. At this step, we can apply current to the LED if we like, and observe light leaking out of the base of the fiber and shining out of its tapered tip.

We applied 30 mA to a blue EZ290 LED and held a 10 mm × 10 mm photodiode 5 mm above fiber tip. We obtained a photocurrent of 1.2 mA, which corresponds to 6.0 mW of blue light. This seemed odd to us, so we repeated the measurement several times. This particular LED was emitting 18 mW at 30 mA, and our calculations based upon the fiber's numerical aperture suggested that no more than 3 mW should be emerging in total from the fiber tip.

We applied clear epoxy (E30CL) to the fiber base, with power still applied to the LED. The intensity of the light emitted by the tip of the taper decreased immediately, while that of the light emitted from the base of the fiber increased. We measured once again the power 5 mm from the tip of the fiber. We observed only 1.5 mW. Later, we measured power emitted in all directions with the same fiber tip and obtained a total of close to 3 mW.

The numerical aperture of an optical fiber is the greatest angle a ray entering a polished, perpendicular face can make with the fiber axis and still be constrained within the fiber by total internal reflection. This total internal reflection can occur at the core-cladding boundary, which is always available, or at the cladding-glue boundary, or the cladding-air boundary. The following calculation shows how the numerical aperture of the fiber is affected by glue and air.



The WF300/330/P37 fiber has a cladding of fused silica, with refractive index n₃ = 1.458. Its specified numerical aperture is 0.37, which is the numerical aperture we get by total internal reflection at the core-cladding interface. The refractive index of the air outside the base of the fiber is n₁ = 1.000. Using the equation derived above, we conclude that the germanium-doped core of the fiber has refractive index n₂ = 1.504. Now suppose we surround the fiber with clear epoxy. Our clear epoxy has refractive index n₄ = 1.5. Because the glue has higher refractive index than the cladding, there will be no internal reflection at the cladding-glue boundary.

When we are assembling a head fixture, we hold the fiber in a clamp that touches the cladding along three contact lines each 5 mm long, so the majority of the cladding surface is exposed to air. Under these conditions, our equation gives us a numerical aperture of 1.1, which we interpret to mean that any ray entering the fiber will be trapped by internal reflection at the cladding-air boundary. Thus we expect to see all the power entering the base of the fiber emerging at the tip. Our fibers were not perfectly clean, so we were losing some light because of oil on the cladding surface, but we do see four times as much power when we hold the fiber without glue in a clamp.

Suppose we use a glue with a lower refractive index than the cladding. We will now see total internal reflection at the cladding-glue interface. Consider the MY132, UV-curing adhesive, designed specifically for cladding optical fibers. It is expensive (roughly $300 for 10 ml). But its refractive index is only 1.324. With this adhesive fastening the fiber to our LED, and coating the fiber up to the base of the taper, the numerical aperture of the fiber would be increased to 0.71, which means that light within a ±46° cone will be accepted and constrained within the fiber.

With numerical aperture 0.37, we expect to capture 14% of the light emitted by an EZ500 LED. This calculation is borne out by our measurements. But with numerical aperture 0.71 we will capture 51% of the emitted light. The power delivered to our fiber tip will increase by almost a factor of four.

We have learned from Cree that their EZ290 LED will not produce the optical power we expected. The most efficient LED we can buy is the EZ500. We believe the most efficient class of these LEDs will emit 30 mW of blue light with forward current 30 mA. A well-positioned 400-μm diameter fiber covers 90% of the light-emitting surface of the EZ500. Thus we can hope for 27 mW to enter our adhesive-coated fiber, and 14 mW to emerge from the tip. We plan to order a reel of the most efficient class of EZ500 LEDs, and a sample of the MY131MC adhesive, and test our hypothesis.

Another way to increase the numerical aperture of the fiber is to increase the refractive index of its core. We have ordered a sample of 1.4-mm diameter borosilicate glass rod from Fiberoptix, which has refractive index 1.6. We will try to stretch this to create a fiber of diameter 400 μm which, when coated by MY132, will provide numerical aperture 0.90 and therefore capture 81% of the LED light. We would then be able to deliver 22 mW to the fiber tip.

Stage Three Delivery

Today we ship to ION the following components:

• 5 of Head Fixture (A3024HF)
• 1 of Implantable Lamp (A3024A)
• 2 of White Test Lamps
• 1 of Command Transmitter (A3023CT)
• 1 of Booster Amplifier (ZHL-3A)
• 1 of 24-V Power Supply for Booster Amplifier
• 1 of Flexible Antenna with 2-dB Attenuator
• 1 of Telescoping Antenna with BNC elbow
• 1 of Coaxial Cable with 12-dB Attenuator

Early next week we plan to ship the following, which will complete the deliveries required by ISL Stage Three, Design and Construction of the Implantable Lamp.

• 4 of Implantable Lamp (A3024A)

In the photograph below, we see the Command Transmitter (A3023CT) connected directly to the Flexible Antenna. The 2-dB attenuator at the base is necessary to stabilize the A3023CT's power amplifier. This arrangement supplies 100 mW of 146-MHz RF power to the antenna, and is easy to set up. We use this arrangement for test that do not require us to operate more than 50 cm from the antenna. We determine the length, number, and spacing of RF power pulses using the same control program that we use with the Lamp Controller (A2060L).



The same photograph shows one Implantable Lamp (A3024A) flashing a white LED, and another at with a paper insulator around its L+ lead. The paper insulation is needed to stop the A3024A contact pins from touching when stored in a bag. If they touch and the lamp is stimulated, we will waste battery capacity supplying current to the lead resistance. The white LED is one of our White Test Lamps, which we have equipped with sockets to accept the pins on the tips of the A3024A leads. The test lamp leads have color codes and socket orientation to mimic the head fixtures and the colors of the A3024A leads.



When we want to operate farther from the antenna, and allow for random movements of the receiver, we add a ZHL-3A booster amplifier between the A3023CT and the antenna, and we use a telescoping antenna instead of the shorter flexible antenna. The telescoping antenna is more efficient. In this arrangement, we must be sure to insert the 12-dB attenuator between the A3023CT and the ZHL-3A, so as to protect the ZHL-3A's input from over-drive. With this arrangement, we obtain 100% reliable stimulation of the implantable lamps at range 1 m in our basement laboratory and 2 m in a faraday tent. This operating range is double that which we set as our target.



The telescoping antenna, being 1 m tall, needs to be vertical or else it will fall over. The ZHL-3A amplifier gets warm after a few minutes. We have found it to be rugged, but the manufacturer recommends that you connect its load (the antenna) and input (the cable carrying 146 MHz) before you connect power (the 24 V supply) in order to protect it from over-drive.

The Head Fixtures (A3024HF) are equipped with sockets for the A3024A contact pins. They are equipped with dummy cannulas in their guide cannulas. We have applied black epoxy over the clear epoxy that holds the fiber to the LED and the circuit board to the guide cannula. The black epoxy serves to mask light that escapes through the base of the fiber, which is roughly 85% of the light emitted by the LED. By masking this light, we are better able to estimate the power emitted by the fiber tip, and we avoid flashing a bright light into the subject animal's field of view, which might otherwise corrupt our experiment. The disadvantage of our black covering of epoxy is that the experimenter may not be able to confirm by inspection whether or not the implantable lamp is responding to commands. In future designs, we will consider placing a separate LED on the back of the head fixture to emit a small amount of light as an indicator for the experimenter.



It is hard to measure the total power emitted in all directions by the fiber tapers. Nevertheless, we tried to do so and obtained 2.5±1 mW. When we tested the fibers before we tapered them, we obtained 3±0.2 mW. These results are consistent, and suggest that the total power is a little below 3 mW. This 3 mW is well below our target of 10 mW. In the future, we will increase the power output at the tip by using a higher numerical aperture fiber, or higher drive current, or a more efficient LED, or some combination of all three modifications.

Prototype Head Fixture

The following photograph shows our first assembled fiber and cannula Head Fixture, following the design we presented earlier. The small ruler graduations are 0.5-mm. The fiber diameter is 300 μm.



Part (4) is the fiber, one end of which is glued with clear optical epoxy to an EZ500 LED mounted on the circuit board. This fiber is a dummy we used to make a prototype head fixture. Its tip is sheared off at an angle instead of tapered with a flame.

Part (1) is the L+ lead from an Implantable Lamp (A3024A). Part (2) is the connector pin on the end of the L− lead from the same device. These pins plug into two sockets on the Head Fixture. Part (3) is the L− socket. The L+ socket is obscured by L−. Part (8) is the head fixture circuit board. Part (5) is a silica guide cannula. Part (6) is the threaded pedestal on the guide cannula. Part (7) is a smoothing capacitor to reduce noise induced in EEG recordings.

Measured Capture Efficiency

We have four different types of optical fiber and two different types of light-emitting diode. We make three samples of each fiber, which we name 1 to 3 for each type. Each fiber has two faces, A and B. We lower each face of each fiber onto an LED in turn and measure the power emerging from the other face.



Figure: Fraction of Power Captured By Fibers. The 480-μ square LED is the C460EZ500. The 290-μm square LED is the C470EZ290.

In the above table, we calculate the theoretical capture fraction in two steps. First, we estimate the fraction of light that will enter the fiber, based upon the area of the fiber and the area of the LED. Second, we apply our cosine-distribution solution to the capture efficiency of a fiber of known numerical aperture, which we present here.

In the case of the 400-μm fiber over the 290-μm square LED, we assume all the LED's light enters the fiber. The fiber is larger than the diagonal of the square, and placed within 50 μm of the LED surface by pressing down the bond wire. We observe 15% capture fraction and calculate 14%. Our calculation based upon the fiber numerical aperture appears to be accurate.

In the case of the 300-μm fiber over the 480-μm LED, we assume that only 30% of the light will enter the fiber. But our observed capture fraction is 9% and our calculation is 5%. Given that we already trust our numerical aperture calculation, we suspect that twice as much light is entering the fiber as we expected, which in turn means that the light emitted by the 480-μm square LED is concentrated towards the center.

When we place a 400-μm fiber with NA = 0.37, NA = 0.25, or NA = 0.24 on the 480-μm square LED, the capture fraction we measure is roughly 1.6 times the one we calculate. This result is also consistent with concentration of light towards the center of the light-emitting area.

Our 300-μ NA = 0.41 fiber's capture fraction with the 290-μm LED is 17%. With a 400-μm, NA = 0.37 fiber on the same LED we get 15%. If we assume that all the light from the LED enters both fibers, then the difference in capture fraction is consistent with our calculation due to numerical aperture. This suggests that the light emitted by the 290-μm LED is also concentrated towards the center, so that all of the light enters the 300-μm fiber.

We conclude that our numerical aperture calculation, which assumes a cosine distribution of light emission by the LED, is accurate, but our assumption of uniform distribution of light across the LED is not. The light is concentrated towards the center of the emitting area. Thus we are able to obtain almost double the capture fraction that we would with uniform light distribution.

With the 300-μm, NA = 0.41 fiber on the EZ290 we get 17% of the light emitted by the LED emerging from the tip of our fiber. If we could obtain a C470EZ290 that emitted 40 mW for 30 mA current, as specified by the data sheet, we would obtain 6.8 mW at the fiber tip. As it is, our EZ290s are producing only 17 mW at 30 mA, so we see only 3.0 mW. We do not know why our EZ290s are performing so poorly. The are emitting less than half the light we expect from the calibration sheet supplied with our samples. It may be that they have aged from exposure to air over the past year and a half since we received them. In the case of the EZ500, the LEDs produce 25 mW for 30 mA current, and we get 11% capture efficiency with our 400μm, NA = 0.37 fiber. So we obtain 2.6 mW at the fiber tip.

As things stand today, we can obtain roughly 3 mW with both the EZ290 and the EZ500, using our high numerical aperture 300-μm and 400-μm fibers respectively.

LED Efficiency

We measure the total power emitted by a selection of LEDs. To measure optical power we use an SD445 photodiode. It's sensitivity to light of various wavelengths, in Ampere per Watt, is given in the figure below. We press the photodiode right up against the package of our LED, so that is roughly 2 mm from the light-emitting surface.



We reverse-biase the photodiode with a 9-V battery and pass the photocurrent through a 100-Ω resistor. We measure the voltage across the 100-Ω resistor with a voltmeter. We convert photocurrent into optical power using the graph above. At 470 nm we use 0.20 A/W. At 527 nm we use 0.25 A/W. We provide power to the LED through a 400-Ω, 1-W resistor. We measure the LED current with an ammeter. We obtain the following plots of output power versus current.



According to the EZ290 data sheet, the minimum power output of the blue C470EZ290-021 at 20 mA forward current should be 21 mA. According to the calibration of our sample diodes, the power should be at least 27 mW for this particular LED. But we measure only 13 mW. According to the same data sheet and calibration, the green EZ290s should produce at least 11 mW at 20 mA. But we measure only 6 mW. The EZ500 data sheet, meanwhile, specifies a minimum of 40 mW of green light at forward current 150 mA. We see 26 mW at 46 mA, which suggesets of order 85 mW at 150 mA.

Our green EZ500 emits twice as much power as we expect, but our blue and green EZ290s appear to be emitting less than half the power we expected from their calibration and specification. The blue EZ290 shown above will emit only 18 mW with a forward current of 30 mA, such as we expect to deliver with our Implantable Lamp (A2024A). Even if we obtain 25% coupling efficiency into our fiber, we will get no more than 4.5 mW out of the fiber tip.

UPDATE: [26-APR-13] We have 25 C460EZ500 (460 nm blue) mounted in 3-mm packages. We measure the light power emitted by one such part with a photodiode. We bias the photodiode with 0 V and with 9 V. The photocurrent is 6% higher with bias. The responsivity of the un-biased photodiode is roughly to 0.182 for 460-nm light and 0.191 mA/mW at 470 nm.

UPDATE: [22-JAN-14] The surface of the SD445 appears to be acrylic glass, which has reflectance with angle of incidence in air as plotted below. We obtained this and the following plot from Refractive Index Info.



The silicon of the photodiode we assume to be crystalline, which has the following reflectance with angle of incidence in air. By reflection alone, we expect to lose around 44% of incident unpolarized blue light by reflection at the acrylic and silicon boundaries for light arriving perpendicular to the surface. We calculate the sensitivity of the ideal photodiode, where one photon becomes one electron, is 0.38 mA/mW for 470 nm. If we lose 44% of incoming photons by reflection, we expect our SD445 to have sensitivity 0.21 mA/mW. The data sheet says 0.20 mA/mW.



At larger angles of incidence, we will lose more light by reflection, so the sensitivity of the photodiode will drop. At 80° we expect to lose around 60% by reflection, compared to 40% at 0°, so sensitivity will drop to 0.13 mA/mW.

Antenna Matching

Today we try a split capacitor antenna matching circuit to see if we can amplify the RF signal on our antenna before presenting it to our detector diode. Such amplification is, in theory, possible, because the source impedance of the antenna signal is of order 100 Ω, this being the resistance of the antenna wire to 146 MHz, while the load impedance of our detector diode is of order 10 kΩ. We describe our analysis and testing of the split-capacitor network in detail here. The following oscilloscope trace shows the dual resonance of the matching circuit we built.


Here we see the detector diode output as a function of frequency when we have a two-loop stainless steel antenna picking up power from a nearby transmitter. The top trace is a frequency sweep voltage. The bottom trace is the detector diode output. The first peak is at 146 MHz and corresponds to a gain of 20 generated by the split capacitor tuning network. Thus the signal applied to our detector diode is twenty times larger in amplitude than the signal on our antenna. The second peak is at 170 MHz and corresponds to the resonance of the antenna inductance with our split capacitor.

We equip an Implantable Lamp (A3024) with the split capacitor circuit and test its reception when transmitting pulses of 146 MHz power at 1.6 W into a half-wave antenna. We find that reception is 100% up to range 3 m, and remains 50% at 14 m. The matching network has increased the effective range of our command receiver by a factor of six. We can now expect 100% reliable reception within a faraday enclosure at up to 1.5 m, which will be sufficient to communicate with the ISL.